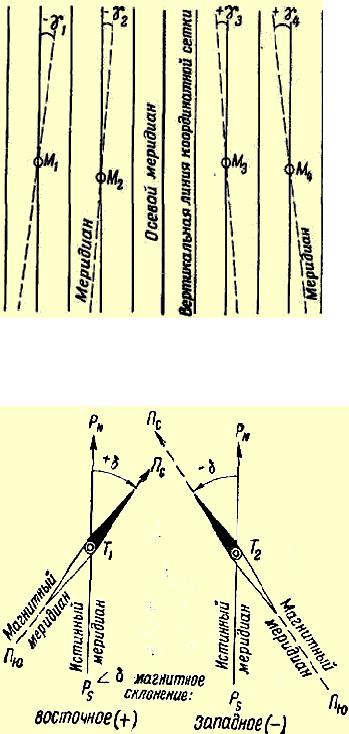
Рис. 62. Склонение магнитной стрелки (магнитное склонение)

4.5.Взаимосвязь между угловыми величинами, применяемыми в топографии.

Рис. 61. Сближение меридианов

греческой буквой γ (гамма).

Вертикальные линии координатной сетки не совпадают с направлениями истинных меридианов, а образуют с ними некоторый угол (рис. 61). Происходит это потому, что меридианы сходятся у полюса в одной точке, в то время как вертикальные линии координатной сетки в пределах каждой зоны остаются параллельными между собой.

Угол между северным направлением истинного меридиана данной точки и вертикальной линии координатной сетки называется сближением меридианов и обозначается

	Из рисунка 61 видно, что
во	всех	точках	осевого
меридиана		сближение	равно
нулю.		Чем	дальше

вертикальные линии отстоят от осевого меридиана зоны, тем этот угол становится больше; на краях зоны он достигает 3 .

Если вертикальная линия сетки отклоняется северным концом к востоку от истинного меридиана, то сближение меридианов считается восточным (со знаком +), при отклонении же в противоположную сторону - западным (со знаком - ).

Истинный меридиан в свою очередь не совпадает с магнитным меридианом. Угол между одноименными направлениями

истинного и магнитного меридианов называется магнитным склонением и обозначается греческой буквой δ (дельта). Склонение считается восточным (со знаком + ), если северный конец стрелки уклоняется к востоку от

Рис. 64. Переход от дирекционного угла к магнитному азимуту и обратно

Рис. 63. Схема магнитного склонения, сближения меридианов и поправки направления, помещаемая на полях карты

истинного меридиана, и западным (со знаком - ) при уклонении к западу

(рис. 62).

В силу магнитных свойств Земли магнитное склонение в различных пунктах земной поверхности неодинаково. На одном и том же месте оно также не остается постоянным, а из года в год изменяется.

Таким образом, из сказанного видно, что вертикальные линии координатной сетки и магнитные меридианы образуют между собой угол. Этот угол называется отклонением магнитной стрелки или поправкой направления (П). Он отсчитывается от северного направления вертикальной линии координатной сетки и считается положительным (со знаком + ), если северный конец магнитной стрелки отклоняется к востоку от этой линии, и отрицательным (со знаком - ) при западном отклонении магнитной стрелки.

Данные о величине поправки направления и слагающих ее величинах сближения меридианов и магнитного склонения помещаются в виде схемы на полях карты, под нижней стороной ее рамки (рис. 63).

Эти данные о поправке направления необходимы для того, чтобы можно было быстро переходить от дирекционных углов, измеренных по карте, к соответствующим им магнитным азимутам и обратно.

Чтобы перейти от дирекционного угла к магнитному азимуту, надо ввести в этот угол поправку направления, т. е. поправку за отклонение магнитной стрелки. При этом если отклонение магнитной стрелки указано на карте восточное (со знаком + ), то поправка вычитается из дирекционного угла, а если западное (со знаком - ), то прибавляется.

Чтобы яснее представить себе при работе на карте переход от дирекционных углов к азимутам и обратно, рассмотрим рисунок 64, на котором показаны шесть основных случаев взаимного расположения направлений магнитного меридиана и вертикальной линии координатной сетки относительно истинного меридиана.

Как видно из рисунка, для всех этих случаев зависимость между различными углами можно представить в виде следующих общих алгебраических формул:

1)	П  ( )  ( )	,

т. е. поправка направления П равна алгебраической разности магнитного склонения δ и сближения меридианов γ (в формуле величины δ и γ заключены в скобки, чтобы показать, что они берутся алгебраически - со своими знаками).

Пример: δ = +5° (восточное); γ = - 1° (западное).

П = + 5° - ( - 1°) = 6°, т. е. отклонение магнитной стрелки будет восточное 6°.

2)	Ам    (П)	,

т. е. магнитный азимут Ам равен алгебраической разности дирекционного угла α и поправки направления П.

Пример: α = 45°; δ = +7°30' (восточное); γ = - 2°30' (западное); Ам = 45° - [ +7°30' - (- 2°30') ] = 35°.

3)	  Ам  (П)	,

т. е. дирекционный угол равен алгебраической сумме магнитного азимута Ам и поправки направления П.

Пример. Ам = 175°; δ = - 4° (западное); γ = +2° (восточное), α = 175° + [- 4° - ( + 2°)] = 169°

Переход от дирекционного угла к магнитному азимуту и обратно применяется главным образом тогда, когда приходится учитывать годовое изменение магнитного склонения. Для этого годовое изменение склонения магнитной стрелки умножают на число лет, прошедшее после создания карты, и полученную величину алгебраически суммируют со значением склонения магнитной стрелки, указанным на карте. Затем переходят от дирекционного угла к магнитному азимуту или обратно по формулам.

Например, на карте измерен дирекционный угол направления α = 134º30´. Известно, что δ 1995 г= -8º16´, γ= -2º13´, годовое изменение склонения восточное 0º05´. Определить магнитный азимут данного направления.

δ 2009 г=-8º16´+(+0º05´·14)= -7º06´ П=δ-γ=-7º06´-(-2º13´)=-4º53´ Ам=α-П=134º30´-(-4º53´)=139º23´.

Указанные выше системы координат определяют плановое положение точек на поверхности земного эллипсоида. Чтобы определить положение точки на физической поверхности Земли, дополнительно к плановому положению указывают ее высоту (отметку) над уровнем моря. В нашей